大白话带你推导UniswapV2公式及分析其代码
什么是UniSwap
uniswap是一个智能合约,实施基于“恒定乘积公式”的自动流动性协议。每个Uniswap交易对上都存储着对于两种资产的储备。可以理解为每个国家都会对其他国家有一定的外汇储备,在兑换对应资产时使用。
UniSwapV1
介绍V2之前,我们先介绍一下uniswapV1。
uniswapV1主要提供各种ERC20 token与ETH互相兑换的途径,以ETH为交易中心来实现ERC20 token与ERC20 token之间的兑换。
可以理解成你拿黄金去换白银,Uniswap V1的兑换方式就是先计算出来1g黄金能换多少美元,再把换出的美元拿去购买白银。
UniSwapV2
UniSwapV2与V1是基于相同的公式实现,但它提出了以下三点创新:
- 支持创建任意ERC20/ERC20的交易对,不再需要以ETH为交易中心媒介。
- 可以理解为你拿黄金换白银不用再用美元作为中介了,可以直接拿黄金换相对应的白银。
- 提供了一个更强的价格预言机,在每个块的开头计算两个资产的相对价格。
- 可以理解为交易所每时每分都在为你更新现在1g黄金对比多少白银
- 支持闪电交换(Flash swap),即闪电贷,用户可以免费的获得这些资产并在链上使用它们,只需要在交易结束后归还这些资产。
- 可以理解为你可以把黄金先免费借出去,然后你再这交易所里可以随意换别的资产,换完只要你能够还回来原本的黄金g数以及利息,剩下多套利的部分就归你所有。
- 这部分知识可以通过学习闪电贷(DEX)来深入了解
概述
在开始解释前,我们通过这张图可以了解到Uniswap在做什么。
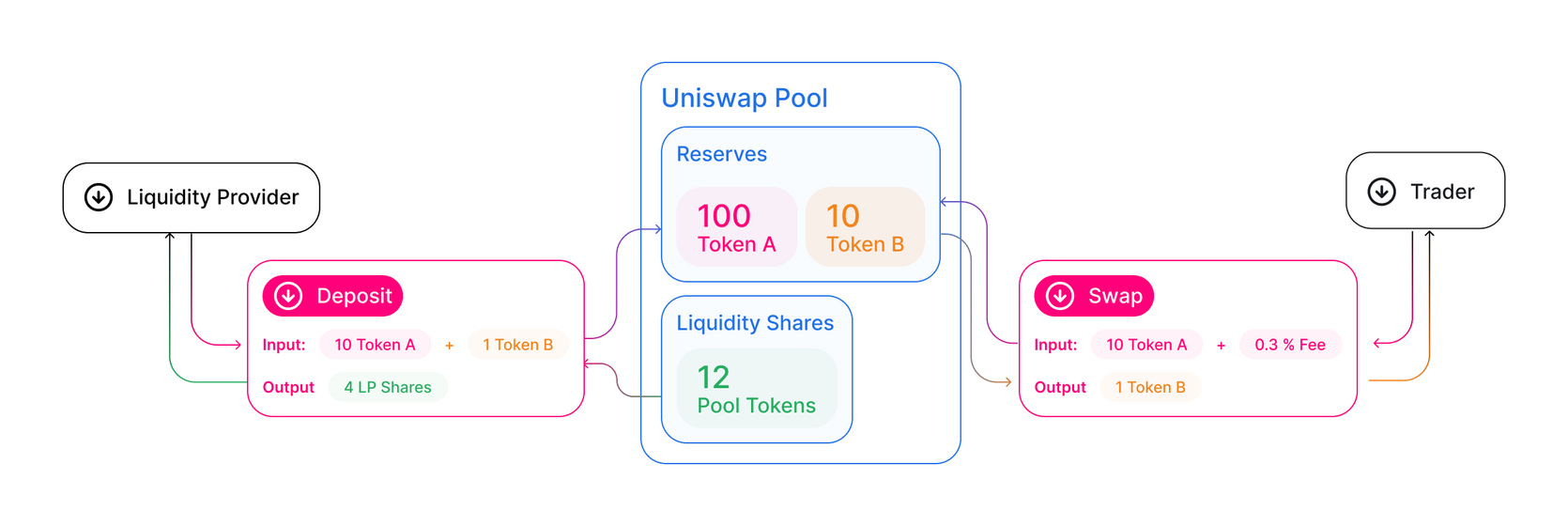
简单来说就是流动性提供者提供token pair并获得LP shares,可以产生持续收益。
交易者将自己想交易的token用uniswap交换到对应token。
恒定乘积公式
要理解Uniswap,就必须理解恒定乘积公式,接下来我会带你推导一遍恒定乘积公式,并试图让你理解为什么这么做。
模型概述
恒定乘积公式$x\times y=k$,
$x$和$y$分别为交易时token $X$和token $Y$的数量。代币兑换价格由$x$和$y$的比率决定,从而保留$x\times y$的乘积。
也就是说,当你出售了$\Delta x$代币时,你将获得$\Delta y$代币,使得
$x\times y = k = (x+\Delta x)\times(y-\Delta y)$
当使用$\Delta y$交易$\Delta x$时,交易代币的储备更新公式如下:
$x' = x+\Delta x = (1+\alpha)x = \frac{1}{1-\beta}x$
$y' = y-\Delta y = \frac{1}{1+a}y = (1-\beta)y$
其中,$\alpha = \frac{\Delta x}{x},\beta=\frac{\Delta y}{y}$。因此我们有了:
$\Delta x = \frac{\beta}{1-\beta}x$
$\Delta y = \frac{\alpha}{1+\alpha}y$
我们这里解释一下上述公式,其中$\alpha=\frac{\Delta x}{x}$以及$\beta = \frac{\Delta y}{y}$的含义是你所交易的token/该token总数。价格$\frac{\Delta x}{\Delta y}是\frac{x}{y}$的函数,我们交易的时候只会给出其中一方的token,假设是$\Delta x$,通过这样的公式计算得出我们应该获得多少对应的$\Delta y$。可以看出,在$\Delta y = \frac{\alpha}{1+\alpha}y$中,计算出$\Delta y$所需要的变量只有$x,y,\Delta x$,这样可以保证你输入$\Delta x$时就能得到相应的$\Delta y$
紧接着,我们考虑每一次token交易时,我们都需要给流动性提供者一笔手续费。手续费在UniswapV2中设置为$\rho = 0.003$。那么我们在有手续费的情况下,交易公式变成了以下:
$x'_\rho = x+\Delta x = (1+\alpha) x = \frac{1+\beta(\frac{1}{\gamma}-1)}{1-\beta}x$
$y'_\rho = y-\Delta y = \frac{1}{1+\alpha\gamma}y = (1-\beta)y$
其中,$\alpha = \frac{\Delta x}{x},\beta=\frac{\Delta y}{y}$,$\gamma = 1-\rho$,因此我们能得出在有手续费情况下的计算公式为
$\Delta x = \frac{\beta}{1-\beta}\cdot\frac{1}{\gamma}\cdot x$
$\Delta y = \frac{\alpha\gamma}{1+\alpha\gamma}\cdot y$
当存在手续费时,即$\rho>0$时,有$x'\rho\times y'\rho > x\times y$。
这里我们完成了基础的恒定乘积公式的推导,后续在核心代码中更详细的部分我们会在下文分析代码时继续详细推导。
代码结构

- UniswapV2 ERC20.sol
- 定义Uniswap的LP token,用于奖励流动性提供者
- UniswapV2Factory
- 负责提供通用的字节码,它的工作时为每一个唯一的token pair创建一个且仅有一个智能合约
- UniswapV2Pair
- 该代码中集成了关于交易token pair的逻辑。
UniswapV2Pair
在V1中,每次流动性交换需要用ETH作为交换桥梁,这样使得交易路由更简单,并减少了流动性的碎片化。但缺点就是对流动性提供者的要求变高了,流动性提供者必须提供ETH。
在V2中,你可以创建任何ERC20 Pair的流动性池,以达到可以直接通过ERC20 token兑换ERC20 token。
swap
在Uniswap代码中,每次swap都会调用该函数:
function swap(uint amount0Out, uint amount1Out, address to, bytes calldata data) ck {
函数接受参数中可以看出,uniswap要求swap的调用者通过amount{0,1}Out参数指定他们希望接收多少个想要的代币,这些输出的代币数量取决于swap调用者输入的token{0,1}。
swap的完整代码如下:

上述代码主要完成的任务就是利用乘积恒等式在你用swap交易token时在余额中更新token数量,并给你对应的token。
- 黄色部分将你要的ERC20发送到你的地址上,如果你有附带的数据说明你要调用什么方法
- 绿色的部分计算剩余的token0和token1代币有多少,如果不够的话,这次转账失败
- 紫色的部分计算扣除相应的手续费,即要给流动性提供者的收益。
值得注意的有两点
- 为了防止浮点数计算,V2中的手续费计算方式由$x' = x-0.03\times\Delta x$变为了$1000\times x' = 1000\times x - 3\times\Delta x$
- 采用了块作用域来解决堆栈过深的问题。
pools
每个Uniswap流动性池都是一堆ERC20 token的交易场所。pool合约创建时,各个代币的余额为0。为了促进交易,必须有人用每个代币的初始存款作为种子。第一个流动性提供者时设定该池初始价格的人。也就是说,第一流动性提供者提供的$x$和$y$会得到最初的$x\times y = k$,后续的流动性波动都是在这基础之上进行波动的。
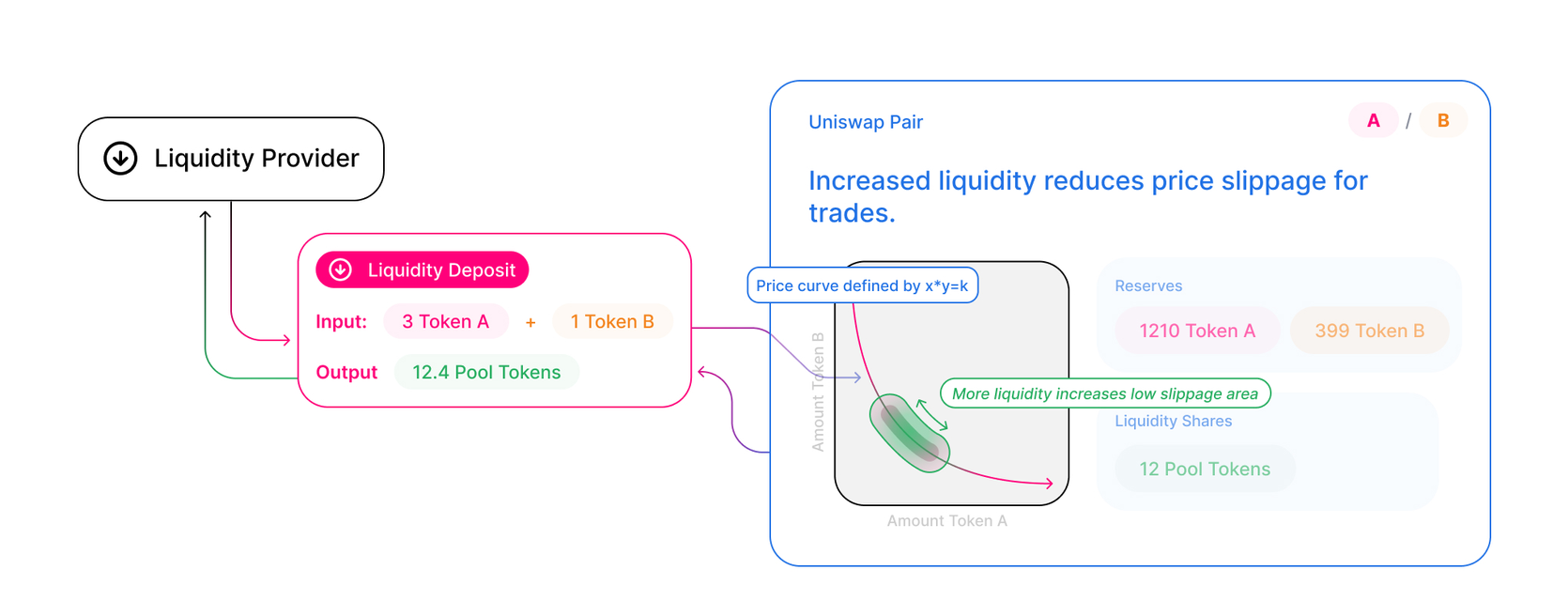 每当有流动性存入池子中,流动性提供者就会获得liquidity token作为奖励。每当发生交易时,该合约都会收取$0.3$%的费用,作为流动性提供者的奖励。
每当有流动性存入池子中,流动性提供者就会获得liquidity token作为奖励。每当发生交易时,该合约都会收取$0.3$%的费用,作为流动性提供者的奖励。
对于最初的流动性提供者,它可以获得$\sqrt{x\times y}$的liquidity token作为奖励,其中一部分奖励以minimum_liquidity的形式永久锁在最初的流动性提供者手中。后续的流动性提供者获得的奖励计算公式为$\min(\frac{x\times totalSupply}{X},\frac{y\times totalSupply}{Y})$.
在代码中体现为:
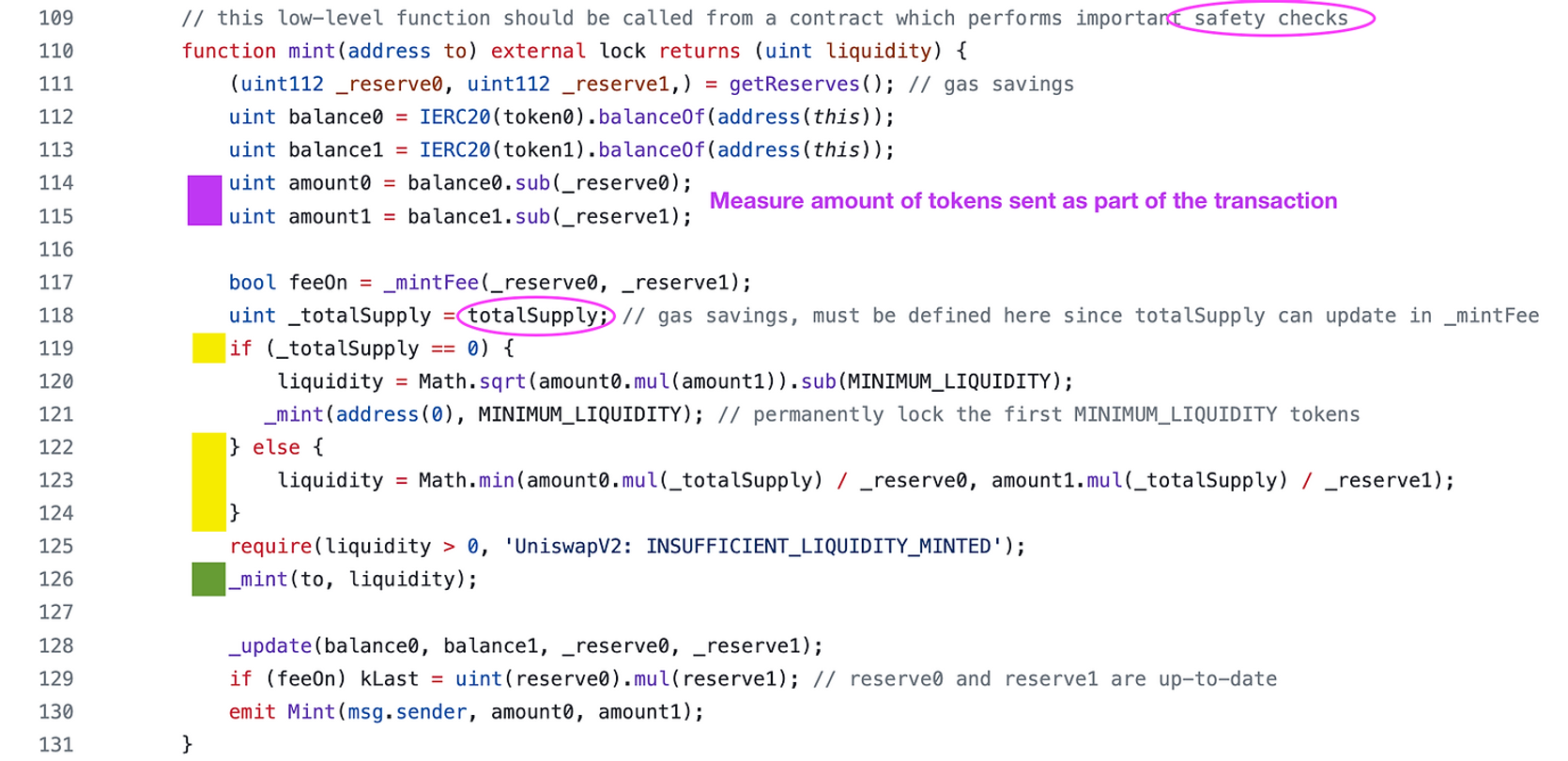
=- 首先我们先关注池子中已经存在流动性的情况。
- 123行。计算流动性,将流动性计算为两个值中的较小者。其中比率$\frac{amount0}{reserve0}$是指按LP token的总供应量缩放。
- 假设有10个token0和1个token1,如果用户提供10个token0和0个token1,则他将获得最小值(10/10,0/10)并获得零个流动性代币。
- 另一个例子,如果用户将token0的供应量增加5%,token1供应量增加10%,那么它只能铸造LP token供应量的5%。
- 用户总是会得到提供流动性比例中最差的一个,这回激励他们增加token0和token1的供应,而不去改变token0和token1的比率,因为改变比率没有任何好处。
- 然后我们再来关注第一铸币者的问题
- 119行值121行。是在新创建池子时,池子流动性为0时第一铸币者的情况
- Uniswap的防御通货膨胀的措施是销毁第一批MINIMUM_LIQUIDITY,以确保没有人拥有LP代币的全部供应,以至于可以轻松操纵价格
 为什么Uniswap要采取乘积的平方根来计算铸造的份额?以下是白皮书的理由
为什么Uniswap要采取乘积的平方根来计算铸造的份额?以下是白皮书的理由
Uniswap v2 最初铸造的份额等于数量的几何平均值,流动性 = sqrt(xy)。该公式确保任何时候流动性池份额的价值本质上与最初存入流动性的比率无关......上述公式确保流动性池份额的价值永远不会低于该储备金的几何平均值水池。
我们用一个例子来看这个事情。
- 假设我们没有使用平方根来衡量流动性,并且我们从池中的10个token0和10个token1开始,之后池中有20个token0和20个token1。
- 从直观上看流动性是增加了一倍,但是如果我们不求平方根,流动性将从$10\times 10=100$最终为$20\times 20 = 400$。这样流动性翻了四倍。这与我们所获得的事实不符。
- 同时在费用上,在开平方下,池子的流动性从100增加到200。流动性提供者的利润是100%,所以他们需要支付成比例的费用。如果不开平方,则是变成了400,需要支付4倍利润的费用。
burn
uniswapV2的生命周期是有人第一次mint了LP token,最终销毁时是在流动性提供者销毁他们的LP token来赎回自己的ERC 20 token。
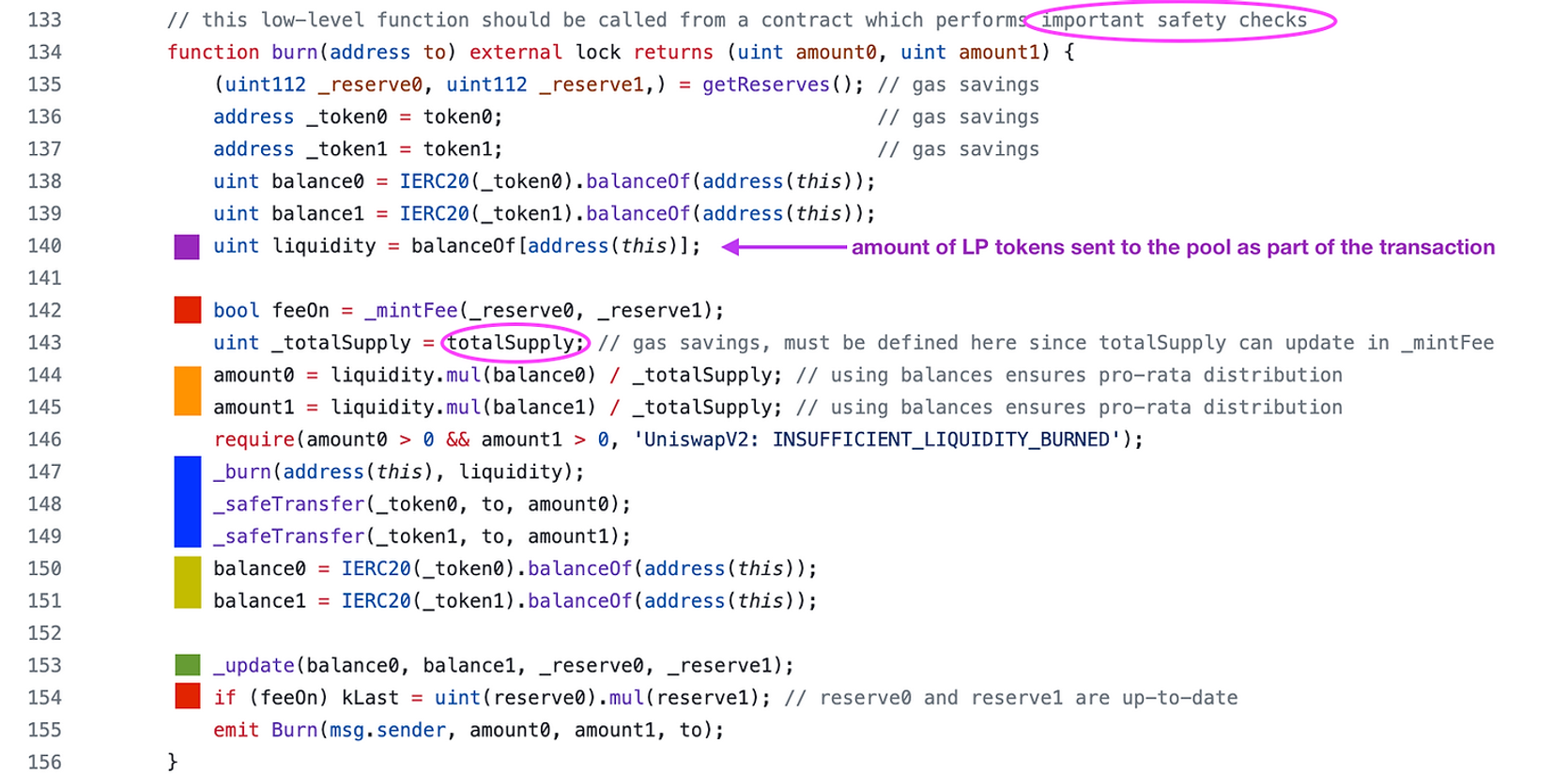
140行用紫色表示。流动性时通过pool合约拥有的LP代币数量来衡量的。用户发送到合约的金额会被销毁。
142行和154行的红框表示费用,我们可以暂时跳过这些费用,因为Uniswap不对流动性提供者收取费用
144行和145行。用于计算LP提供者将收回多少金额。如果流动性代币的总供应量是1000个,他们燃烧100个LP代币,那么他们将获得池中持有的token0和token1的10%。流动性/总供应量是他们在LP代币总供应量中燃烧的份额。
147到149行。是LP token被销毁,token0和token1被发送回流动性提供者的账户上
150行到151行。更新余额变量。
153行,调用_update函数更新TWAP和_reverse变量
价格预言机 Price Oracle
价格预言机时用于查看给定资产价格相关信息的工具,比如你在手机上看股票价格的时候,手机就可以被称作为价格预言机。然而在链上时没有办法实时感知外部世界的,因此不同的链上的价格预言机都带有不同的设计与不同的去中心化程度。
UniswapV2给出的办法是,在任何交易发生之前,都会计算每个区块开始时的市场价格。由于这个价格是由前一个区块中的最后一笔交易决定的,因此这个价格的操纵成本很高。攻击者必须在前一个区块的最后一笔交易进行恶意交易,但是这也不能保证攻击者能正好在下个区块获利,除非攻击者拥有的算力能够连续开采两个区块。
但是单凭这样还是有风险,UniswapV2将结束价格添加到核心合约中的单个累计价格变量中,并按照价格存在的时间进行加权,该变量代表合约的历史记录中每秒Uniswap价格的总和。 
外部合约可以使用该变量来跟踪任何时间间隔内准确的时间加权平均价格(TWAP)。
TWAP 是通过在所需时间间隔的开始和结束时读取 ERC20 代币对的累积价格来构建的。然后,可以将该累积价格的差异除以间隔长度,以创建该期间的 TWAP。
也就是说,这样可以通过时间来把攻击者的篡改造成的危害降到最低,除非攻击者能够每次都篡改成功,不然uniswap的价格不会产生大幅波动。

TWAP 可以直接使用,也可以根据需要作为移动平均线(EMA 和 SMA)的基础。
- 对于 10 分钟 TWAP,每 10 分钟采样一次。对于 1 周的 TWAP,每周采样一次。
- 对于简单的 TWAP,操纵成本随着 Uniswap 上的流动性以及平均时间长度的增加(近似线性)而增加。
- 攻击的成本相对容易估计。将价格在 1 小时 TWAP 上移动 5% 大约等于套利损失的金额以及在 1 小时内每个区块将价格移动 5% 的费用。
这部分在代码中体现为:


- 黄色部分计算经历了多少个时间单位,时间单位以出块计算
- 绿色部分计算对应的价格累加量
- 紫色部分更新信息,更新最后一次计算的时间,以便下次计算
Uniswap Factory
Uniswap Factory对每一个ERC20 token pair 池创建一个智能合约,其核心逻辑如下,代码比较简洁,这部分不做过多介绍

Flash Swap
Uniswap 闪电掉期允许您提取 Uniswap 上任何 ERC20 代币的全部储备,并无需预付费用即可执行任意逻辑,前提是在交易结束时您可以:
- 使用相应的配对代币支付提取的ERC20代币
- 返还提取的 ERC20 代币并支付少量费用
任何人都可以通过闪电贷的方式在去中心化的交易所中套利,获得套利空间。这样可以更好的让每个token pair的汇率保持在他们应有的水平。因为只要出现token pair的汇率与大众预期不符,或者与其他交易所相差过大,就会有人用闪电贷的方式套利,促使价格回归正常区间。
版权声明
本文仅代表作者观点,不代表区块链技术网立场。
本文系作者授权本站发表,未经许可,不得转载。
 区块链技术网
区块链技术网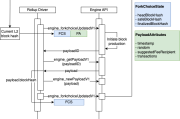




发表评论:
◎欢迎参与讨论,请在这里发表您的看法、交流您的观点。